Spread polynomials
In the conventional language of trigonometry, the nth-degree spread polynomial Sn, for n = 0, 1, 2, ..., may be characterized by the trigonometric identity
Although that is probably the simplest way to explain what spread polynomials are to those versed in well-known topics in mathematics, spread polynomials were introduced by Norman Wildberger for use in rational trigonometry, a subject in which one generally avoids the sine function and the other trigonometric functions of angles. The angle at which two lines meet is determined by a rational function of their slopes, known as the spread between the two lines. The spread is equal to the square of the sine. The rational function can be identified without mentioning the sine function; see rational trigonometry for more on this.
Contents |
Identities
Explicit formulas
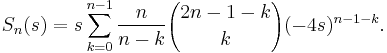 (S. Goh)
(S. Goh)
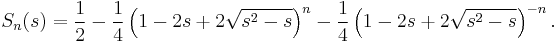 (M. Hovdan)
(M. Hovdan)
From the definition it immediately follows that
Recursion formula
Relation to Chebyshev polynomials
The spread polynomials are related to the Chebyshev polynomials of the first kind, Tn by the identity
This implies
The second equality above follows from the identity
on Chebyshev polynomials.
Composition
The spread polynomials satisfy the composition identity
Coefficients in finite fields
When the coefficients are taken to be members of the finite field Fp, then the sequence { Sn }n = 0, 1, 2, ... of spread polynomials is periodic with period (p2 − 1)/2. In other words, if k = (p2 − 1)/2, then Sn + k = Sn, for all n.
Orthogonality
When the coefficients are taken to be real, then for n ≠ m, we have
For n = m, the integral is π/8 unless n = m = 0, in which case it is π/4.
Generating functions
The ordinary generating function is
The exponential generating function is
Differential equation
Sn(s) satisfies the second order linear homogenous differential equation
Use in rational trigonometry
Rational trigonometry is a recently introduced approach to trigonometry that eschews all transcendental functions (such as sine, cosine, etc.), all measurements of angles or compositions of rotations, and characterizes the separation between lines by a quantity called the "spread", which is a rational function of the slopes. Equality of angles between rays entails equality of spreads between lines. The spread between two lines is the square of the sine of the angle. The name "spread polynomials" comes from the use of these polynomials in rational trigonometry.
Table of spread polynomials, with factorizations
The first several spread polynomials are as follows:
- Failed to parse (PNG conversion failed;
check for correct installation of latex, dvips, gs, and convert): \begin{align} S_0(s) & = 0 \\[10pt] S_1(s) & = s \\[10pt] S_2(s) & = 4s-4s^2 \\ & = 4s(1-s) \\[10pt] S_3(s) & = 9s-24s^2+16s^3 \\ & = s(3-4s)^2 \\[10pt] S_4(s) & = 16s-80s^2+128s^3-64s^4 \\ & = 16s(1-s)(1-2s)^2 \\[10pt] S_5(s) & = 25s-200s^2+560s^3-640s^4+256s^5 \\ & = s(5-20s+16s^2)^2 \\[10pt] S_6(s) & = 36s-420s^2+1792s^3-3456s^4+3072s^5-1024s^6 \\ & = 4s(1-s)(1-4s)^2(3-4s)^2 \\[10pt] S_7(s) & = 49s-784s^2+4704s^3-13440s^4+19712s^5-14336s^6+4096s^7 \\ & = s(7-56s+112s^2-64s^3)^2 \\[10pt] S_8(s) & = 64s-1344s^2+10752s^3-42240s^4+90112s^5-106496s^6 \\ & {} \qquad + 65536s^7-16384s^8 \\ & = 64s(s-1)(1-2s)^2(1-8s+8s^2)^2 \\[10pt] S_9(s) & = 81s - 2160s^2 + 22176s^3 - 114048s^4 + 329472s^5 - 559104s^6 \\ & {} \qquad + 552960s^7 - 294912s^8 + 65536s^9 \\ & = s(-3+4s)^2(-3+36s-96s^2+64s^3)^2 \\[10pt] S_{10}(s) & = 100s - 3300s^2 + 42240s^3 - 274560s^4 + 1025024s^5 \\ {} & \qquad - 2329600s^6 + 3276800s^7 - 2785280s^8 + 1310720s^9 - 262144s^{10} \\ & = 4s(1-s)(5 - 20s+16s^2)^2(1-12s+16s^2)^2\\[10pt] S_{11}(s) & = 121s - 4840s^2 + 75504s^3 - 604032s^4 + 2818816s^5 \\ {} & \qquad -8200192s^6 + 15319040s^7 - 18382848s^8 + 13697024s^9 -5767168s^{10} + 1048576s^{11}\\ & = s(11 -220s + 1232s^2 -2816s^3 +2816s^4 -1024s^5)^2 \end{align}
References
- Wildberger, N.J., Divine Proportions : Rational Trigonometry to Universal Geometry, Wild Egg Books, Sydney, 2005
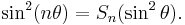
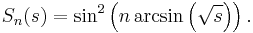
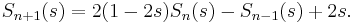
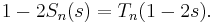
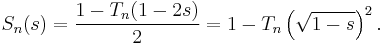
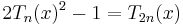
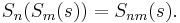
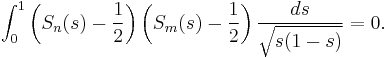
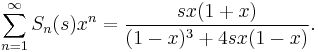
![\sum_{n=1}^\infty {S_n(s)\over n!} x^n = {1 \over 2} e^x \left [ 1-e^{-2sx} \cos\left (2x \sqrt{s(1-s)}\right )\right ] .](/2012-wikipedia_en_all_nopic_01_2012/I/f50b02688e86ec4cdbaca997899b6a8e.png)